Grandes matemáticos que aportaron a la geometría analítica

Pierre de Fermat

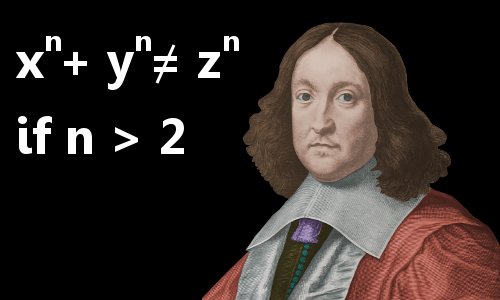
Pierre de Fermat

Tomado de https://www.famousscientists.org/images1/pierre-de-fermat.jpg

(Beaumont, Francia, 1601 - Castres, id., 1665) Matemático francés. Continuador de la obra de Diofanto en el campo de los números enteros y cofundador del estudio matemático de la probabilidad, junto con Pascal, y de la geometría analítica, junto con Descartes, Pierre de Fermat mantuvo correspondencia con los grandes científicos de su época y gozó ya en vida de gran estima e inmensa reputación, si bien su natural modestia y su modo de trabajar, en exceso diletante, perjudicó la divulgación de sus aportaciones.

Las primeras aportaciones de Pierre de Fermat datan de 1629, cuando abordó la tarea de reconstruir algunas de las demostraciones perdidas del matemático griego Apolonio de Perga relativas a los lugares geométricos; a tal efecto desarrollaría, contemporánea e independientemente de René Descartes, un método algebraico para tratar cuestiones de geometría por medio de un sistema de coordenadas, de capital importancia para la constitución de la geometría analítica. Sirviéndose de los símbolos de François Viète, trató ampliamente la ecuación de la recta, y las de la hipérbola, la parábola y la circunferencia.

Fermat se sitúa asimismo entre los matemáticos que dieron el primer impulso al cálculo infinitesimal, y fue el primero en estudiar las cuestiones de máximo y mínimo (desde 1636) con el método que hoy llamamos de las "derivadas",

 En el ámbito de la óptica geométrica, formuló principio de Fermat, que deduce las leyes de la reflexión y la refracción. En 1654, y como resultado de una larga correspondencia, desarrolló con Blaise Pascal los principios de la teoría de la probabilidad.

En relación a la teoría de  de números realizó aportes importantes relacionados con las propiedades de los números primos, muchas de las cuales quedaron expresadas en forma de simples proposiciones y teoremas.

Y además creo el teorema de Fermat, que afirma  que la ecuación xⁿ+yⁿ=zⁿ no tiene solución entera positiva si el valor del exponente n es superior a 2.

Rene Descartes

(La Haye, Francia, 1596 - Estocolmo, Suecia, 1650) Filósofo y matemático francés. Después del esplendor de la antigua filosofía griega y del apogeo y crisis de la escolástica en la Europa medieval, los nuevos aires del Renacimiento y la revolución científica que lo acompañó darían lugar, en el siglo XVII, al nacimiento de la filosofía moderna.

 

 René Descartes

Tomado de http://www.citatecelebre.eu/imgupl/author/t-600x600/rene-descartes--167.jpg

 En 1628 decidió instalarse en Holanda, país en el que las investigaciones científicas gozaban de gran consideración y, además, se veían favorecidas por una relativa libertad de pensamiento. Descartes consideró que era el lugar más favorable para cumplir los objetivos filosóficos y científicos que se había fijado, y residió allí hasta 1649.

En 1637 apareció su famoso Discurso del método, presentado como prólogo a tres ensayos científicos. El método cartesiano, que Descartes propuso para todas las ciencias y disciplinas, consiste en descomponer los problemas complejos en partes progresivamente más sencillas hasta hallar sus elementos básicos.

Los fundamentos de su física mecanicista, que hacía de la extensión la principal propiedad de los cuerpos materiales, fueron expuestos por Descartes en las Meditaciones metafísicas (1641), donde desarrolló su demostración de la existencia y la perfección de Dios y de la inmortalidad del alma, ya apuntada en la cuarta parte del Discurso del método. El mecanicismo radical de las teorías físicas de Descartes, sin embargo, determinó que fuesen superadas más adelante.

Descartes es considerado como el iniciador de la filosofía racionalista moderna por su planteamiento y resolución del problema de hallar un fundamento del conocimiento que garantice su certeza, y como el filósofo que supone el punto de ruptura definitivo con la escolástica. En el Discurso del método (1637), Descartes manifestó que su proyecto de elaborar una doctrina basada en principios totalmente nuevos procedía del desencanto ante las enseñanzas filosóficas que había recibido.

 Recuperado de :

https://www.biografiasyvidas.com/biografia/f/fermat.htm

https://www.biografiasyvidas.com/biografia/d/descartes.htm